⇐ Previous Article — Table of Contents — Next Article ⇒
New Energy Times home page

Ekström Energy Analysis of Rossi Device

Appendix 2 to New Energy Times Report #3

(See related Appendix 24)

Source: http://www.fysik.org/WebSite/fragelada/resurser/coldfusionkrivit.pdf
[The version below contains minor edits for clarity.]

New Energy Times Reporting From Bologna
By Peter Ekström, Lund University

I think Steven Krivit’s video from his visit to Bologna is very revealing [1]. In that video [1a], viewers can see a little puff of mist at the end of the tube. If there were invisible steam rushing out of the tube at a speed of 11 m/s [Calculation 1], the puff of mist would certainly be blown away quickly.

According to Andrea Rossi, the E-Cat is putting out 5 kW power. Therefore, according to Rossi, what we see coming out of the tube is the total production of the E-Cat, running at 5 kW.

The little trickle that is visible in the video is hardly useful for heating or producing electricity. Note that losses in the tube are small according to Rossi [1b] and that all water is converted into dry steam [Calculation 2].

Where does the power go? Out of the E-Cat? Not likely, because it is well-insulated. Out of the hose? Not very likely because the thermal losses are small; 5 kW is a lot of power to lose, and it would heat the room perceptibly.

The only remaining explanation is that the E-Cat does not produce excess energy. The input electrical power is 3.5*220=770 W [2b]. It takes 608 W to heat 7 kg of water in one hour from 25ºC to 100ºC [Calculation 2]. The remaining 770-608=162 W is used to evaporate a small fraction of the water.

Because the temperature of the output water is not actually measured [see addendum 2011-06-30], it is quite possible that the temperature is less than 100ºC, which would leave some additional power to evaporate water.

So where is the water then? It should be trickling out of the tube. When Rossi removed the end piece of the tube, he very deliberately emptied a fair portion of water from the tube, and he subsequently held the end above the level of the rest of the tube [1c]. It would take significant time for the tube to be filled with water, and the water would trickle out [Calculation 3].

Addendum 2011-06-29
Rossi claims that 100% of the water is evaporated. In his response to the initial version of this document [3], he claims that the losses through the tube are 5.4 kW.

Because the total output power is 5.0 kW, the thermal efficiency is negative. A very strange machine! Rossi claims that the losses result from radiative losses from the tube. Let’s use the Stephan-Boltzmann law to calculate the radiative power if the tube radiates as a blackbody (maximum radiation).

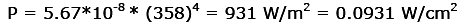
The temperature was taken as 85°C = 358 K. The result is far less than the value 1 W/cm^2 claimed by Rossi. Either Rossi is wrong about radiation losses, or he has discovered a new radiation law.

The obvious explanation is, of course, that the E-Cat produces no excess energy, which explains the limited power visible at the end of the hose.

The above result becomes even more striking if the tube does not behave as a blackbody (it doesn’t) and if we also consider radiation from the room.

Of course, everyone knows that the main energy loss in normal circumstances is by convection. It is, even so, inconceivable that the total loss from the tube is much more than 500 W. This would, if the E-Cat produces 5 kW, leave plenty of energy to be dissipated at the end of the tube. We see nothing of this in the video [1].

Addendum 2011-06-30
A reader questioned what I meant by “Since the temperature of the output water is not actually measured, it is quite possible that the temperature is less than 100ºC.”

First, this is of course only speculation. Depending on the construction of the water cooling system, it may be possible that some water escapes into the drainage tube before it has reached 100ºC (uneven heating of the input water).

In that case, a reader might argue, there would be more power to evaporate more water. This is not a very important part of my reasoning – the 162 W above is enough to produce some steam, definitely an amount consistent with what viewers can see in the video.

Addendum 2011-07-01
Here is a still picture of the end of the hose. Near the end of the hose, the steam is invisible, but within a few centimeters, it is virtually stopped and becomes visible because of condensation. It is hard for me to imagine that the steam comes out with a speed in excess of 10 m/s. According to calculation 1, the volume/s of dry steam coming out should be 3.4 l/s. This is definitely not what we are seeing.

References
1. Krivit’s video: http://www.youtube.com/watch?v=m-8QdVwY98E
1a. Steam against T-shirt: 11.30
1b. "very small condensation": 10.40 (minutes.seconds)
1c. The tube trick: 11.00
1d. "In this moment we are making 7 kilograms of water per hour": 12.15
2. Rossi calculates: http://www.youtube.com/watch?v=YrTz5Bq6dsA
2a. Temperature difference: 3.35
2b. Ampére meter: 09.20
3. Rossi Response to Ekstrom

Brief Biography of Peter Ekström (Sweden)
Peter Ekström is the deputy head of the Nuclear Physics Division, Department of Physics, Lund University, Sweden http://www.pixe.lth.se/staff/staffSearch.asp?ID=3

⇐ Previous Article — Table of Contents — Next Article ⇒